kirşof kanunu

Elektrik

Kirşof (Kirchoff) Kanunu

Kirşof gerilim kanunu ile;

devreye uygulanan gerilim, dirençler üzerinde düşen gerilimlerin toplamına eşittir diye ifade etmiştir.   Kirchhoff Yasası seri, paralel ve karmaşık elektrik devrelerinin analizinde kullanılan, elektrik enerjisi ve yükünün korunumuna dayalı, ilk kez 1845 senesinde Gustav Kirchoff tarafından tanımlanan iki eşitliktir. Kirşof (Kirchoff) kanunu akım ve gerilim durumlarını inceler. Kirşof (Kirchoff) kanunu Ohm kanunu’ nun tamamlayıcısıdır.

Kirşof Kanunu ikiye ayrılır.

1. Kirşof Akımlar Kanunu (Birinci Kirşof Kanunu),
2. Kirşof  Gerilim Kanunu (İkinci Kirşof Kanunu)

Kirşof Akımlar Kanunu 

Kirşof akımlar kanunu ile; bu kanun aynı zamanda birinci kanun ve düğüm kanunu olarak da adlandırılır. Bu kanuna göre herhangi bir düğüm noktasına gelen akımların toplamı, çıkan akımların toplamına eşittir.

Daha teknik anlamda Kirchhoff’ un akımlar kanunu, Ampere yasasının diverjansı ve Gauss yasasının birleştirilmesi ile şu şekilde elde edilir:

Birinci kanun, yük korunumunun açıklamasıdır. Herhangi bir noktaya ne kadar akım girerse, o kadar da terk etmek zorundadır.

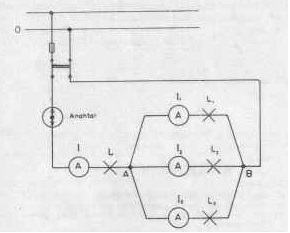
Kirchhoff’ un akımlar kanunu, akımla ile ilgili bir kanundur. Birinci kanunu açıklamak için aşağıdaki şeklimizdeki gibi bir elektrik devresi kuralım. Lambalar 25 W’ lık olsun. Devreyi kapatacak olursak (I) ampermetresinin gösterdiği değer kollara bağlanan üç ampermetrenin gösterdiği değerlerin toplamını gösterir.

Birinci Kirşof Kanunu (Kirşof Akımlar Kanunu)

Bu deneyden çıkarılan sonuçları tanımlarsak; 

1. Üreteçten çekilen akım A noktasında kollara ayrılmıştır.
2. Her koldan, bu kolun direnci ile ters orantılı değerde bir akım geçmektedir.
3. Kollardaki akımlar B noktasında birleşirler, ana koldaki (A noktasındaki)akımı meydana getirirler.

Bu açıklamaların doğrultusunda Kirchhoff’ un akımlar kanunu’ nu tanımlayabiliriz:

Ana koldan geçen akım şiddeti, kollardan geçen akım şiddetlerinin toplamlarına eşittir. Diğer bir ifadeyle akımın kollara ayrıldığı düğüm noktasına gelen akım ile bu noktadan ayrılan akımların matematiksel toplamı sıfırdır.

Bu anlattıklarımızı bir bağıntı halinde yazarsak;

I = I1 + I2 + I3 +……  Kirchhoff’ un akımlar kanunu’ nu bu formül ile ifade etmiş oluruz. Düğüm noktasına gelen ve ayrılan akımlara göre formül yazmak istersek;

I- (I1+I2+I3+…………….) =0 olur.

Akımın kollara ayrılması

Uygulama: Şekilde görüldüğü gibi bir 0 düğüm noktasına gelen akım şiddetleri I₁=1 A, I₂ = 4 A, bu noktadan ayrılan kollardaki akım şiddetleri I₃ = 1 A, I₄ = 2 A, I₅ = 2 A olduğuna göre bu devreye Kirchhoff’ un akımlar kanunu’ nu uygulayabiliriz: Gelen akımlar      I_Ge = I₁ + I₂ = 1 + 4 = 5 A Ayrılan akımlar   I_Ay = I₃ + I₄ + I₅ = 1 + 2 + 2 = 5 A olur. Bir düğüm noktasında; gelen akım ayrılan akıma eşit olduğundan:

1_Ge = I_Ay

I₁ + I₂ = I₃ + I₄ + I₅

1 + 4 = 1 + 2 + 2 olur.

Kirşof Gerilim Kanunu 

İkinci Kirşof Kanunu (Kirşof Gerilim Kanunu)

İkinci Kirşof kanunu elektrik gerilimi ile ilgili bir kanundur. Yukarıdaki şeklimizde görüldüğü gibi lamba, havya ve ocağı birbirine seri olarak bağlayalım. Bu devreye bir gerilim uygulayalım. Devre elemanlarını meydana getiren lamba, havya ve ocakta düşen gerilimleri ölçmek için her birine paralel ayrı ayrı voltmetreler bağlayalım. Uyguladığımız gerilimi ölçmek için ise bu elemanların hepsine paralel bir voltmetre bağlayalım. Devreye gerilim uyguladığımızda elemanlara bağladığımız voltmetrelerin gösterdikleri değerlerin toplamı; uygulanan gerilimi, okuduğumuz voltmetrenin gösterdiği değere eşit olduğu görülür. Şeklimize göre 220 Voltluk gerilimle beslenen bir devrede üç alıcının bağlandığını göstermektedir. Lamba, havya, ocağın dirençleri bilindiğine göre devreden geçen akımla bu dirençleri çarpacak olursak Ohm Kanunu’ na göre;

U₁ = I . R₁,  U₂= I . R₂,  U₃= I . R₃ bulunur.

Bunlar elemanlardaki gerilim düşmesini göstermektedir. Bunların toplamı ise devreye uygulanan gerilime eşit olacağından:

U=  + U₂ + U₃ = I . R₁ + I .         R₂ + I . R₃= I . (R1 + R2 + R3)

U = I . (R₁ + R₂ + R₃) olur. Burada R= R₁+R₂+R₃ dür.

U = I . R olur. Bu duruma göre Kirchoff’ un Gerilim Kanunu’ nu tanımlayabiliriz: Kapalı bir elektrik devresine uygulanan gerilim, bu devrede yer alan alıcıların uçları arasındaki (elemanlarda düşen gerilimler) gerilimlerin toplamına eşittir. Bu anlattıklarımızı bir bağıntı halinde ifade etmek istersek U = U₁ + U₂ + U₃ +……….Kirşof Gerilim Kanunu formülünü elde ederiz. Bu formülü gereğinde; U – (U₁ + U₂ + U₃) = 0    şeklinde de yazabiliriz. Bu ifade ise bize bir elektrik devresinde gerilimlerin matematiksel toplamının sıfır olduğunu ispat eder.

• Kirchoff  Kanunu’ nun Seri Devreye Bağlanması 

Yukarıda şekilde görüldüğü gibi lamba, havya ve ocak devreye seri bağlanmış yani bunların dirençleri de devreye seri girmiştir. Ampermetre ve voltmetreleri de şekilde görüldüğü gibi bağlayalım. Şimdi direnç, akım ve gerilim durumlarına dikkat edelim.

Direnç durumu; Dirençlerin seri bağlandığı bir devredeki toplam direnç, dirençlerin toplamına eşittir.

R = R₁ + R₂ + R₃ +……. olur.

Akım durumu; Seri bağlanan dirençlerin uçlarına bir gerilim uygulanacak olursa her dirençten geçen akım şiddeti birbirinin aynı olur.

Devrenin her noktasında I = I oluyor demektir.

Gerilim durumu; Seri bağlanan dirençlerin her birinden aynı miktar akım geçer ve direncin değerine göre bir gerilim düşmesi meydana gelir. Seri dirençlerde ki gerilim düşmelerinin toplamı devreyi besleyen gerilime eşit olur.

U = U₁ + U₂ + U₃ +…… olur.

• Kirşof Kanunu’ nun Paralel Devreye Bağlanması

Şekilde olduğu gibi alıcıları devreye paralel bağlayalım ve ampermetre ve voltmetreleri görüldüğü gibi yerleştirelim. Şimdi direnç, akım ve gerilim durumunu inceleyelim.

Kirşof Kanunlarının Paralel Devrelere Bağlanması

Direnç durumu; Devrenin toplam direncinin tersi, dirençlerin terslerinin toplamına  eşittir.

1/R_T = 1/R₁ + 1/R₂ +… olur.

Bir elektrik devresinin direncini azaltmak gerekirse dirençleri paralel bağlamak gerekir.

Akım durumu; Her alıcı direncine göre akım çekeceğinden ana koldaki akım şiddeti, kollardaki akım şiddetleri toplamına eşit olur.

I = I1 + I2 + ….. olur.

Gerilim durumu; Paralel bağlı alıcılarda her alıcının, her iki ucu arasındaki gerilim, devreyi besleyen gerilimin aynıdır.

U = U₁ = U₂

• Kirşof Kanunu’ nun Karışık Devreye Bağlanması 

Alıcıların karışık bağlanması demek, devrede seri ve paralel bağlanmış alıcıların bulunması demektir. Aşağıdaki şekilde karışık bağlanmış bir elektrik devresini göstermektedir. Şimdi bu devre de direnç, akım ve gerilimin durumlarını inceleyelim.

Kirşof Kanunlarının Karışık Devrelere Bağlanması

Direnç durumu; Devrenin toplam direnci, devreye giren seri devre direnci ile paralel devre direnci toplamına eşittir.

R_T = R_S+R_P

R_T = R₁+ (R₂ . R₃) / (R₂ + R₃) olur.

Akım durumu; Ana koldaki akım şiddeti, kollardaki akım şiddetleri toplamına eşittir.

I = I₁ + I₂

Gerilim durumu; Şekilde görüldüğü gibi R₁ direnci devreye seri, R₂ ve R₃ dirençleri birbirlerine paralel bağlanmıştır. Bu üç direncin meydana getirdiği devre bir karışık devredir. Bu karışık devreye uygulanan gerilim (U)’ dur. Değeri ise seri devredeki gerilim düşmesi olan (U₁) ile, paralel devredeki düşen (U₂) geriliminin toplamına eşittir:

U = U₁+ U₂

Kirşof Kanunu Örnek Sorular ve Çözümleri

Soru; 12 voltluk bir akümülatöre dirençleri R₁ = 2 Ω     R₂ = 2 Ω      R₃ = 4 Ω    R₄ = 6 Ω olan 4 far paralel olarak bağlanmıştır.

1. Her farın çektiği akımı
2. Aküden çekilen akımı bulunuz

• Çözüm:

U = 12 V,  R₁  = 2Ω    R₂ = 2 Ω       R₃ = 4 Ω         R₄ = 6 Ω

I = ?      I₁ =?      I₂ = ?      I₃ = ?      I₄ = ?

Her farın çektiği akım;

I₁ = U / R₁ = 12 / 2 = 6 amper

I₂ = U / R₂ = 12 /2 = 6 amper

I₃ = U / R₃ = 12 / 4 = 3 amper

I₄ = U / R₄ = 12 / 6 = 2 amper

Aküden çekilen akım;

I = I ₁+ I₂ + I₃ + I₄

I = 6 + 6 + 3 + 2

I = 17 amper

Soru:

Bir üretece paralel bağlı 4 alıcı 24 amper akım çekmektedir. Alıcıların dirençleri:

R₁ = 1 Ω,      R₂ = 2 Ω,      R₃ = 3 Ω,      R₄ = 6 Ω   olduğuna göre

1. Üretecin gerilimi
2. Alıcıların herbirinin çektiği akımı bulunuz.

• Çözüm:

I = 24 Amper     R₁  = 1Ω    R₂ = 2 Ω       R₃ = 3 Ω         R₄ = 6 Ω

U = ?      I₁ =?      I₂ = ?      I₃ = ?      I₄ = ?

Üretecin gerilimini bulmak için önce devrenin toplam direncini bulmamız gerekir.

R = 1 / 1 / R₁ + 1 / R₂ + 1 / R₃ + 1 / R

  R = 1 / 1 / 1 + 1 / 2 + 1 / 3 + 1 / 6

R = 0,5 Ω

U = R . I = 0,5 . 24 = 12 V

Alıcıların herbirinin çektiği akım;

I₁ = U / R₁ = 12 / 1 = 12 amper

I₂ = U / R₂ = 12 /2 = 6 amper

I₃ = U / R₃ = 12 / 3 = 4 amper

I₄ = U / R₄ = 12 / 6 = 2 amper

Sağlaması

I = I₁ + I₂ + I₃ + I₄                          

I = 12 + 6 + 4 + 2 = 24 amper olur.